（1.3）一般实信号

　　由于信号的偶分量与奇分量是唯一确定的，即
　　实信号f(t)＝实偶信号f_e(t)＋实奇信号f_o(t)
　　FT的线性：　　　　 -> F()＝F_e()＋F_o()
　　性质(1.1)与(1.2)： -> F_e()为实偶函数，F_o()为虚奇函数
　　FT的唯一性： 　　　-> R()＝F_e()，X()＝F_o()

所以，实信号的傅里叶变换的实部R()是偶函数，而虚部X()是奇函数。利用此性质，可得

　　
即 ，此种性质称为偶共轭对称性。由此可知：实信号的FT具有偶共轭对称特性。前面所证明的实偶信号与实奇信号的频谱特点与此是完全符合的。

　　由此性质可得: (1)|F()|=F()F^*()=F^*(-)F(-)=|F(-)|，即实信号的频谱幅度偶对称；(2) (-)=-()，即实信号的频谱相位奇对称。

上面第(2)点证明如下:

　　将频谱函数写成模与相位的形式，则
　　　　F(-)的相位函数为j(-)
　　　　F^*()的相位函数为-j() <- 这可根据复数求共轭的特性而得
　　由于F(-) = F^*()，于是
　　　　(-) = -()
　　证毕.

好啦，下面我们来看看f(t)是虚函数时的FT频谱情况。

(2) f(t)为虚函数

　　对虚函数的FT，下面我们换个方法讨论，目的是想拓宽大家的思路。

　　由于虚函数满足f(t)=-f^*(t)，按上一节所学的FT的共轭特性，得
　　　　　　　　　　　　F()=-F^*(-)

　　上式表明，当f(t)是虚信号时，其频谱F()是共轭反对称的，也称奇共轭对称性。于是
　　R()+jX() = -[R(-)+jX(-)]^*=-R(-)+jX(-)
　　因此，R()=-R(-), X()=X(-)
　　上式表明，当f(t)是虚信号时，其频谱实部R()是奇函数，虚部X()是偶函数。

　　同时还可得 |F()|=|F(-)|, () = - (-)

　　上式表明，当f(t)是虚信号时，其频谱幅度仍是的偶函数，而相位的对称关系则如上式所示。

　　有了上面关于一般虚信号FT频谱的性质，下面两个特殊情况下的结论就不难得到证明了。请大家自己试着证证看。在此就不再赘述了。

　　(2.1) 若f(t)为虚奇信号，则其频谱F()为实奇函数。

　　(2.2) 若f(t)为虚偶信号，则其频谱F()也为虚偶函数。

　　[注释] 虚信号的频谱特性还可仿照实信号的情况进行讨论如下
对于虚函数f(t)，令f(t)=jg(t)，其中g(t)是实函数。则f(t)的FT为


　　
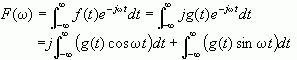
　　显然

　　在这种情况下，R()是的奇函数，X()是的偶函数。
　　利用此性质，可得

　　　F(-)=R(-)+jX(-)=-R()+jx()=-F^*()

　　即F(-)=-F^*()，此种性质称为奇共轭对称性。由此可知：虚信号的FT具有奇共轭对称特性。