2.7.2 反褶与共轭性

　　设f(t)的傅里叶变换为，下面我们来讨论信号反褶、共轭以及既反褶又共轭后，新信号的傅里叶变换。

　　（1）反褶

　　f(-t)是f(t)的反褶，其傅里叶变换为

　　

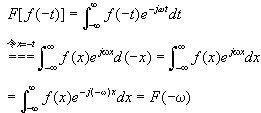
　　（2）共轭

　　

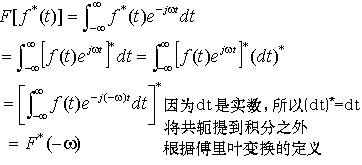
　　（3）既反褶又共轭

　　

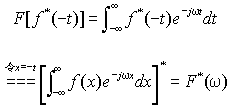
本性质还可利用前两条性质来证明：

　设g(t)=f(-t)，h(t)=g*(t)，则

　

在上面三条性质的证明中，并没有特别指明f(t)是实函数还是复函数，因此,无论f(t)为实信号还是复信号，其傅里叶变换都满足下面三条性质

　　　　　　　　

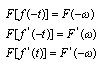
2.7.3 奇偶虚实性

　　已知f(t)的傅里叶变换为。在一般情况下，是复函数，因此可以把它表示成模与相位或者实部与虚部两部分，即

　　
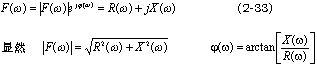
　　根据定义，上式还可以写成

　　

　　下面根据f(t)的虚实性来讨论F()的虚实性。

　　(1) f(t)为实函数
　　对比式(2-33)与(2-34)，由FT的唯一性可得

　　

　　（1.1）f(t)是实的偶函数，即f(t)=f(-t)

　　X()的积分项是奇函数，而奇函数在对称区间内的积分为零，故
　　这时X()=0，于是
　　　　　
　　可见，若f(t)是实偶函数，则F()也是实偶函数，即

　　　左边反褶，右边共轭

　　（1.2）f(t)是实的奇函数，即-f(t)=f(-t)
　　R()的积分项是奇函数，而奇函数在对称区间内的积分为零，故
　　这时R()=0，于是
　　　　　　　　　　　
　　可见，若f(t)是实奇函数，则F()是虚奇函数，即

　　　　左边反褶，右边共轭

有了上面这两条性质，下面我们来看看一般实信号（即可能既不是偶信号，又不是奇信号，反正不清楚，或者说是没有必要关心信号的奇偶特性）的FT频谱特点。