2.5.3矩形脉冲信号

　　矩形脉冲信号的脉宽为、脉高为E，其表达式为，其波形如图2-9(a)所示。可以求得其傅里叶变换为

　　　　

　　上式中的jEsin(t)项在对称区间内的积分为零，去掉了。

　　　　　

　　这样，矩形脉冲信号的幅度谱和相位谱分别为

　　

　　可以看出，矩形脉冲信号的频谱是实函数，可以用同时表示幅度谱和相位谱，矩形脉冲信号及其频谱如图a和图b所示。

　　　　　　　　图2-9 (a)信号波形 (b)信号频谱

　　综上所述，虽然矩形脉冲信号在时域集中于有限的范围，然而它的频谱却分布在无限宽的频率范围上，并按规律变化，其主要能量处于 范围之内。

2.5.4符号函数

　　符号函数表达式为

　　　　　　　　　　

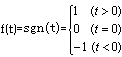
　　显然，这种信号不满足绝对可积条件，但它却存在傅里叶变换，有时这种傅里叶变换称为广义傅里叶变换。

　　要求f(t)的傅里叶变换，可借助于符号函数与双边指数函数相乘，即

　　　

可以求得乘积信号的FT为
　　
于是符号函数的FT为

　　

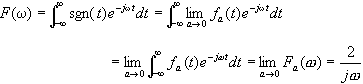
其幅度谱和相位谱分别为：

　　

　　符号函数f(t)与乘积信号的波形与频谱如图所示，其中实线对应符号函数，虚线对应乘积信号。我们可以看出，随着a->0，虚线逐渐向实线靠近。

　　
　　　　　　　　图2-10 (a) 信号波形 (b) 信号频谱