2.4.2 傅里叶变换FT的定义

　　至此，我们利用周期信号的傅里叶级数通过求极限的方法得到非周期信号频谱函数表示式。为区别于傅里叶级数频谱，我们称这种由周期信号的FS通过极限方式导出的非周期信号频谱表达式为连续时间傅里叶变换，简称连续傅里叶变换或傅里叶变换，也有的书上称之为傅里叶积分。其中，（2-32a）称为傅里叶正变换，，简记为FT；（2-32b）称为傅里叶逆变换，也称为傅里叶反变换，简记为IFT。即正变换FT为

　　　　　　
　　　　　
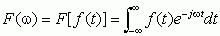
反变换IFT为

　　　　　

通常，称F为f(t)的频谱函数或f(t)的傅里叶变换，有时也记作F(jw)。称为的原函数或傅里叶反变换。

2.4.3 FT与IFT的特性

　　下面我们来看看FT与IFT有些什么特性。

　　从上述关于FT与IFT的定义，我们可以看出：

（1）FT与IFT具有唯一性。即，若两个函数的FT或IFT相等，那么这两个函数必然相等。
（2）FT具有可逆性。即，若F[f(t)]=，则必有；反之亦然。
信号的傅里叶变换一般为复值函数，可以写成

　　　　　　

式中||是的模，代表各频率分量的相对幅度值，称为信号的幅度频谱密度函数，简称幅度谱(函数)，它与的关系称为非周期信号的幅度频谱，是频率的连续函数，其形状与相应的周期信号的频谱包络线相同。而是的相位，表示各频率分量之间的相位关系，称为信号的相位频谱密度函数，简称相位谱(函数)，它与的关系称为非周期信号的相位频谱。

　　既然一般是复函数，我们也可以将它分解下列形式

　　　　　　F() = R() + jX()

其中，R()和X()分别是F()的实部和虚部。

　　与周期信号的FS一样，傅里叶变换也可写成三角形式，即

将上面两式比较后，可得




由上式可知，当f(t)为实函数时
　　　　　　　R()=R(-)，X()=X(-)
　　　　　　　|F()|=|F(-)|，

可见，对于实函数的傅里叶变换来说，它的实部是偶函数（偶对称），而虚部则是奇函数（奇对称）；其幅度谱偶对称（偶函数），相位谱奇对称（奇函数）。

2.4.4 FT存在的充分条件

　　上面的推导和定义看起来很完美，是吗？我不知道大家发现问题没有，事情真的这么简单吗？好象有点儿问题。

　　我们必须指出的是，从理论上来讲，傅里叶变换也应满足一定的条件才能存在。这个条件与周期信号展开成傅里叶级数的狄义赫利条件是相似的，不过非周期信号的时间范围由一个周期变成了无限的区间。FT存在的充分条件是：

　　在无限区间内，信号满足绝对可积，即

　　　　　

　　但这只是充分条件，而并非必要条件。我们以后会发现，一些不满足绝对可积条件的信号同样存在FT。特别是一些不满足上述条件的奇异函数存在FT，使得以后的理论研究更加方便。