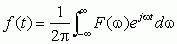将趋于零。这样，周期信号的离散频谱将变成为非周期信号的连续谱。下面，我们把非周期信号视为是周期
趋于无穷大时的周期信号，从而能利用已有的关于周期信号的FS表示式来对非周期信号进行频谱分析。真的能这样对非周期信号进行分析吗？有人可能已经发现这里有一个问题。别着急!下面我们就来仔细探讨一下非周期信号的频谱分析问题。什么？你觉挺对的，没问题？好好，我们大家且往下看。
2.4.1非周期信号的频谱密度
前面我们说，谱线将随信号周期
的不断增大而密集起来，进而成为连续的谱。但是，谱线间隔变为零的时候，谱线的长度也变成了零！即设周期信号傅里叶级数复指数形式为
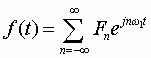
相应的FS系数为
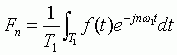
可以看出，当
趋于无穷大时，系数Fn的值趋于零。这种谱怎么表示啊？这就是用FS来对非周期信号进行分析时所面临的问题。换句话说，按FS的分析方法所得的频谱化为了乌有，失到了应用的意义。但是，（1）从物理意义上来考虑，既然成其为信号，则它必然会含有一定的能量，无论信号如何分解下去，其所含的能量是不会消失的。所以，不管周期增大到多大，信号的频谱分布依然应存在。（2）从数学角度来看，在极限情况下，无限多的无穷小量之和，仍可能等于一个有限值，它将与信号的能量有关。这第二句话为什么这么讲？它的背后是有所指的。指的是什么？下面我们就会看到。
基于上述原因，为了表达非周期信号的频谱特性，引入频谱密度函数的概念。令
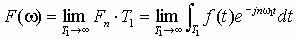
当
时，
不为零，可表示为
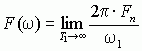
由上式可以看出，
反映的是单位频带内的频谱值，所以称为频谱密度函数，简称频谱函数。于是
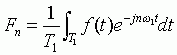
前面说过，非周期信号的周期是无穷大，我们下面来看看在周期无穷大时，上式发生了什么变化。
当重复周期
趋于
时，重复频率
趋于零，谱线间隔
趋于
，离散频率
变成连续频率
，于是上式可写成
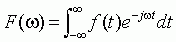(2-32a)下面我们来看看傅里叶级数展开式又会发生什么变化。换句话说，就是有了这个频谱密度式，我们来看看如何用它来表示原信号。
由于
，故傅里叶级数表示式可写成
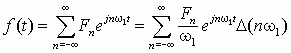
当
趋于无穷大时，上式中各参量有如下变化：
离散值变成了连续值
变化量变成了积分变量
求和变成了积分于是，f(t)的傅里叶级数展开式变成积分形式，即
