上式最后一步的推导过程为：

　　
　　
　　
　　
　　

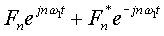
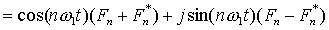
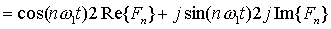
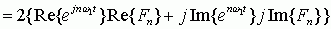
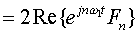
式中，Re{ }表示对括号内的函数取实部，

下面，将Fn以复数形式表达，写成幅度与复指数的表示式如下：

　　若令

　　

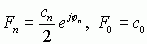
其中Cn为实数，将上面的表示式代入(2-21)，得

　　
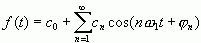
　　若令

　　

其中an、bn为实数，将上面的表示式代入(2-27)，得

　　

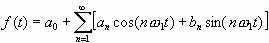
　　(b) 若f(t)为纯虚数，则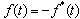 ，于是

因此，当f(t)为纯虚数时，其系数

　　　　（2-28）

　　上式表明，虚数周期信号的傅里叶系数是共轭反对称的，将式(2-28)代入复指数级数展开式(2-23)中，得




式中，Im{ } 表示对括号内的函数取虚部。

这最后一步的推导过程可以参照前面式(2-27)的推导过程，类似进行。

　　若令

　　　　　

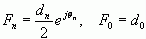
　　假定dn为实数，得

　　　　

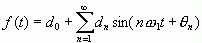
　　总结前面的推导过程，可得Fn与其他傅里叶系数的关系如下：

　　
　
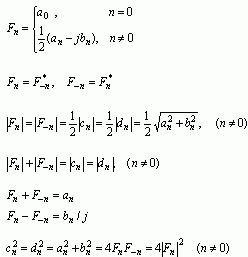
(3) 两种形式的频谱间的关系

　　比较图2-1和图2-2可以看出，这两种频谱表示方法实质上是一样的，其不同之处在于：图2-1中每一条谱线都代表一个分量的幅度，而图2-2中的每个分量的幅度被分成了两半，分别出现在正负频率的相对应位置上，因此，只有把正、负频率上对应的这两条谱线加起来才代表一个分量的幅度。

　　需要指出的是，为什么在复数频谱中会出现负频率呢？这是因为一旦将sin(n1t)、cos(n1t)写成指数形式，以数学的观点来看(根据欧拉公式)，自然而然地就会被分成 两项，从而引入了-jn1t项(即负频率项)。因此，从这个意义上说，负频率的出现纯粹是数学运算的结果，并没有什么物理意义，只有把负频率项与相应的正频率项成对地合并起来，才能得到实际的频谱函数。


2.3.4 具有对称性的周期信号的FS

　　如果给定的周期信号是实信号，而且满足某种的对称性，则求出的傅里叶系数有些项将会为零，从而使运算比较简便。信号波形的对称性有两种：一种是整周期对称，如偶信号和奇信号；另一种是半周期对称，如奇谐信号。下面分别进行讨论。

(1) 偶信号的FS

　　由于f(t)是偶信号，所以是偶函数，而则是奇函数，考虑到在对称区间内积分时，奇函数的积分为零，我们很容易得到以下一组公式



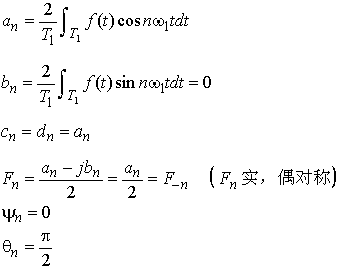
　　从这些公式，我们可以看出，偶信号的FS系数只有直流项和余弦项。换句话说，就是大家在求这类信号的FS时，不用考虑其正弦项对应的系数了。

(2) 奇信号的FS

　　奇信号的FS求法与偶信号的FS求法是类似的。

　　由于f(t)是奇信号，所以是奇函数，而则是偶函数，考虑到在对称区间内积分时，奇函数的积分为零，我们很容易得到以下一组公式

　

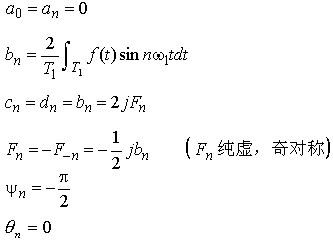
　　从上面的公式，我们可以看出，奇信号的FS系数只有正弦项。这样，如果我们要求奇信号的FS，则可以只求其正弦项系数即可，不必管其它。

(3) 奇谐信号的FS

　　什么是奇谐信号啊？这个名字怎么来的呀？好，我们下面来看看。先来看什么样的信号被称为"奇谐信号"。

　　如果信号f(t)的前半周期波形沿时间轴平移半个周期T1/2后，再关于时间轴作上下翻转，所得波形与原波形一样，即满足

　　

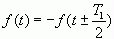
则称此信号为半波奇对称信号，或称为奇谐信号。

　　由于奇谐信号关于时间轴的这种对称性，易知它的FS的直流分量应为零。

　　为了更便于看清奇谐信号的性质，我们来求其复指数形式的FS系数Fn




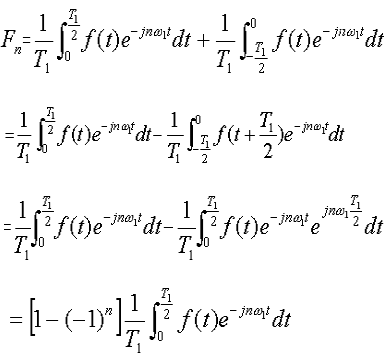
由上式可知，只有当n为奇数时，Fn才存在，即只有n为奇数的复指数分量。

　　下面我们来看看三角形式FS的系数计算公式：

　　(a) n为偶数时（含n=0）：视n=0为n是偶数的一种特例，以便记忆

　　an=bn=0

　　(b) n为奇数时：

　　

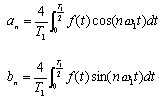
　　通过以上的分析可以看到，奇谐信号的傅里叶级数中，只包含基波和奇次谐波的正弦、余弦项，而不存在偶次谐波项，这也是"奇谐信号"得名的来由。应当指出奇谐信号与奇信号不同，因为前者(奇谐信号)仅包含正弦与余弦的奇次项，而后者(奇信号)包括各次正弦项。

　　另外，满足的信号称为偶谐信号。偶谐信号的最小周期实际上为，它的傅里叶级数包括了的偶倍数次正弦、余弦项。在兴趣的同学可以自己试着推导推导。此处不再赘述。

2.3.5 周期信号的傅里叶频谱

　　本节将以周期矩形脉冲为例，对周期信号的FS频谱进行更深入的讨论。

　　例2.1：设周期矩形脉冲信号的波形如下图所示，脉冲信号的脉宽为t，脉高为E，周期为，在一个周期内的表达式为

　　　　

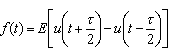
试求其复指数形式和三角形式的傅里叶展开形式与系数。


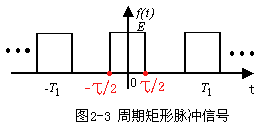
　　解：

　　(a) 若将其展开成指数形式的FS，则系数为

　　
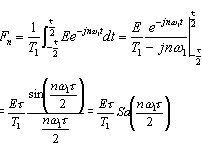
　　上式中的Sa函数是实偶的，所以Fn也是实偶函数。信号f(t)的展开式为

　　

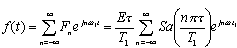
　　(b) 因为信号显然是实偶函数，因此其三角形式的FS展开将只有直流分量和余弦分量，即展开形式为

　　
　　下面我们来求其中的系数a0、an.

　　相应的傅里叶系数为

　　　　

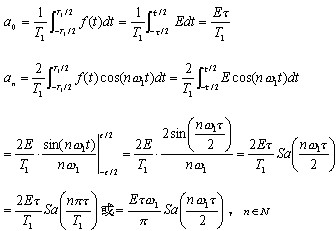
　　这样，周期矩形脉冲信号的三角形式傅里叶展开为

　　　　　

　　上式与合并同频率项写成余弦形式的展开式是一样的，因而相应的系数cn（n=0, 1, …）也就是与an（n=0, 1, …）是一一对应的了。

　　上面我们讨论了信号的展开形式与相应的FS系数，下面我们来看看不同形式下所得FS系数的频谱图，研究一下它的频谱特点。

　　利用前面所得结果，可以画出信号的幅度谱和相位谱 （如下图所示）

　
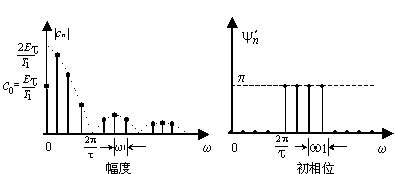
　　　图2-4 周期脉冲信号的三角形式的FS幅度谱和相位谱

以及信号的复数幅度谱及其相位谱（如下图所示）


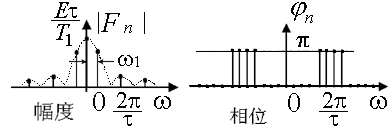
　　　图2-5 周期矩形脉冲信号的复指数形式的FS幅度谱和相位谱

　　由于系数与都是实数，其相位只有0与，分别对应系数的正和负，所以可以将幅度谱与相位谱画在一张图上，用系数的正负来表示（暗示、隐含表示）相应相位是0还是。下图是的幅度与相位合画图。

　　
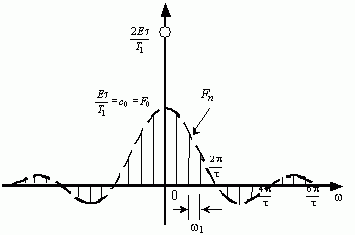
　　图2-6 周期矩形脉冲信号的复指数形式的FS的幅度谱和相位谱

　　好啦！下面我们来看看这些谱图有些什么特点，它们与以前我们知道的一般周期信号的频谱图的特点是不是相吻合的。

　　分析上面的谱图，我们可以发现，周期矩形脉冲信号的FS谱有如下特点：

　　(1) 和一般周期信号的频谱一样，具有离散的频谱，相邻谱线的间隔为。所以，脉冲重复周期T1愈小，则谱线愈疏；反之，T1愈大，则谱线间隔愈小，频谱愈密。当T1趋向无穷大时，谱线间隔趋向于零（最后就成了连续的了），这时的信号实际已经是非周期信号了，而其频谱也成了连续频谱。关于非周期信号的傅里叶分析方法，我们将在下一节里学习。

　　(2) 频谱的幅度包络线按规律变化，其过零点(即跨过横轴的点，此处对应的分量系数为零)可如下确定(其中为谱线间隔)：

　　由Sa函数的性质，过零点位置满足　

　　当Sa函数的自变量等于k时（原点除外），Sa函数取值为零，所以：

　　　　

　　即当时，系数为零。

(3) 信号频谱的谱线有无限多条，即信号可以分解为无限多个频率分量。这些分量的幅度随着频率的增加而减小，其信号能量主要集中在第一个零值点以内。在允许一定失真的条件下，通常只需传送频率范围内的各频率分量就能满足通信系统的要求了。因此，通常把 这段范围内称为矩形脉冲信号的频带宽度，简称带宽，简记为B，即

　　　　　　　　　 （2－31）

显然，带宽只与信号的脉宽成反比，而与脉高和周期均无关。当脉冲宽度变窄时，其频谱包络线零值点的频率愈高，即信号的带宽愈大，频带内所含的分量愈多。

　　在后面我们将对一般信号定义它的等效脉宽和等效带宽。它们之间也是反比的关系。这实际上蕴含着这样的规律：(1) 压缩信号的持续时间（等效脉宽），必然导致其频谱(等效带宽)扩张，反之亦然，两者不可能都很窄或都很宽。(2) 另外，这还说明：信号的持续时间愈短(或在时域上变化愈快)，则它所含的频率分量就愈多! 换句话说，就是时域的激烈变化处(或跳变处)将对应很多(或无限)的频率分量。现在大家对这些内在规律的理解不一定深刻，没关系，学到后面我们就会体会这些规律之间的千丝万缕的内在联系了。希望大家届时能融会贯通。