2.3.2 复指数形式的FS

　　若选用复指数正交函数集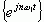来进行傅里叶级数展开，则符合狄义赫利条件的周期函数可以展开成复指数形式的FS

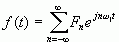　　　　 　　　(2-23)
　　根据有关前面正交函数的讨论，系数Fn可通过下面的公式来求

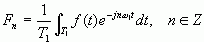　　　　　　　(2-24)
上式的积分区间常取。

　　同样的，我们也可以画出复指数形式表示的信号频谱。由于分量系数Fn一般为复数，故这种频谱称为复数频谱。各分量的幅度和相位与频率的变化关系如图2-2所示：

　　大家要注意：由于复指数展开形式中的FS系数一般是复数，因此图2-2中所画的幅度谱是系数的模|Fn|与的关系。

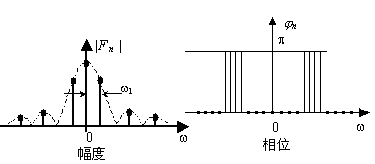
　　　　图2-2 周期信号的复指数形式FS频谱示例

2.3.3 两种傅里叶级数展开形式之间的联系

(1) 由三角形式推得复指数形式

　　根据欧拉公式，利用三角形式的FS系数可以求出复指数形式的FS系数。其推导过程如下

　
　　　(欧拉公式)
　　
　　
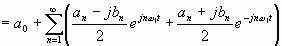
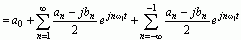　　　(根据an和bn的奇偶性)

　　与式(2-23)比较，可以得到，

　　
　　
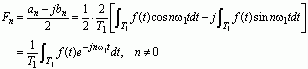
　　上面两个式子可以统一表达为

　　　(2-25)

(2) 从复指数形式推得三角形式

　　(a) 假定f(t)为实数(即f(t)为实周期信号)，则，于是



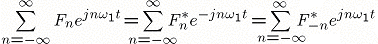
　　第一项等于f(t)，第二项等于f(t)的共轭，第三项是对第二项进行了变量替换：n->-n。对应项相比，可得

　　因此当f(t)是实数时，其复指数FS系数

　　　　(2-26)

　　上式说明，实周期信号的傅里叶系数是共轭对称的。

　　将式(2-26)代入复指数级数展开式(2-23)中，得

　　
　　　将n的正负项分开
　　 　将(2-26)结论代入
　　 　　　　　　　(2-27)