合并时所要用的有关三角公式如下：

　　
　　
　　
　　
　　
　　
　　

　　根据三角公式，可以得到这些傅里叶系数之间的关系为

　　
　　
　　
　　
　　
　　

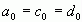
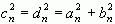
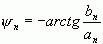
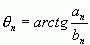
　　根据这些计算公式可知，系数a_n、b_n、c_n及相位_n与n₁是对应的。其中的关系如图2-1所示。从图中我们可以清楚地看出各频率分量的相对大小，这种图称为信号的幅度频谱，简称幅度谱。图中每条线表示某一频率分量的幅度称为谱线，此外还可以画出各分量的相位与n₁的关系，这种图称为相位频谱，简称相位谱。
　　

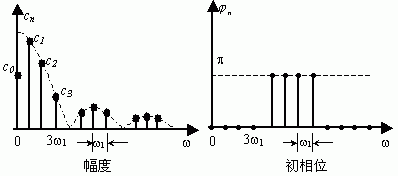
　　　　　　图2-1 周期信号的三角形式FS频谱示例

　　需要特别指出的是，（可能我们的同学自己已经发现了）周期信号的频谱只会出现在整数倍的频率点上，所以这种频谱被称为离散谱，即周期信号的频谱是离散频谱，离散间隔就是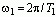。这是周期信号频谱的主要特点。

　　为什么周期信号的频谱是离散的呢？因为周期信号用无穷的谐波来表示，这些分量的频率都是基频的整数倍，不会有其它频率，所以对应到频率轴上，就只是一些离散的点了。

　　另外，离散间隔为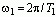，它只与信号的周期有关，换句话说，就是信号的时域周期决定其频域的离散间隔。

　　为了便于记忆，我们把上述特点总结为：周期->离散，它有两层含义，（1）周期信号对应离散频谱；（2）周期大小决定（频谱的）离散间隔。从现在起，大家要让这个特点在脑子里"根深蒂固"，要形成"条件反射"。学到后面，就明白这么做的好处了。