从物理意义上讲，傅里叶级数展开是周期信号在三角函数集这个完备正交函数集上进行的一种信号的正交函数分解。由于正弦信号和余弦信号都是单一频率信号，因此这种分析方法也可以看成是按频率对信号进行分解的一种方法。(这些概念是我们在本门课程的第一章中学习到的。)而如果从纯数学的意义上讲，傅里叶级数展开是周期函数用三角函数的无穷级数来表示，是数学分析的一种方法(或者说，大家不用学这门课就应知道如何做。)。
下面我们分别以三角函数和复指数函数来进行傅里叶级数的讨论。
2.3.1 三角形式的FS
周期为T1的周期信号f(t)，满足狄义赫利条件，就可以展开成三角形式的傅里叶级数
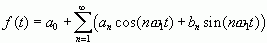(2-17)其中，
是信号的角频率，而an和bn为傅里叶级数系数，简称傅里叶系数。利用式(2-7)，可以求出这些分量系数为：
(a) 余弦分量系数(对应频率或角频率 )
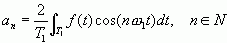(2-18)(b) 正弦分量系数(对应频率 或角频率 )
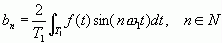(2-19)(c) 直流分量(对应零频率)
(2-20)要说明的是，上面式子的积分区间常取
。这里，式(2-17)是用正余弦信号分量(我们可以把直流分量看成是余弦分量的特例)的线性组合来表示原始信号，通常称为综合公式，而式(2-18)~(2-20)则是由原始信号求它的正余弦信号分量，通常称为分析公式。
上面的式子表明，任何满足狄义赫利条件的周期信号都可以分解为直流和许多正弦、余弦分量，其中第一项a0为常数，它是周期信号中所包含的直流分量，式中的正弦、余弦分量的频率必定是频率
的整倍数。一般把f1称为基频，而把频率为f1的分量称为基波，频率为
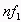的分量称为n次谐波。如果将同频率的正余弦项合并，则可以得到
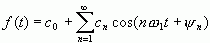(2-21)或
(2-22)