2.2.3 正交函数集
设有函数集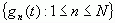 ,在
,在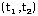 区间上满足
区间上满足
 (2-4)
(2-4)
其中
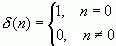 (2-5)
(2-5)
则称该函数集为正交函数集。大家要注意,这里的![]() (n)是单位冲激序列,而不是单位冲激函数
(n)是单位冲激序列,而不是单位冲激函数![]() (t),我们将在"离散时间信号的Z变换"一章中详细讨论它。
(t),我们将在"离散时间信号的Z变换"一章中详细讨论它。
如果将任意一个函数f(t)在区间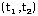 内利用此函数集内的n个函数的线性组合来表示,即
内利用此函数集内的n个函数的线性组合来表示,即
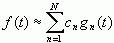 (2-6)
(2-6)
当要求均方误差最小时,各正交分量的系数为
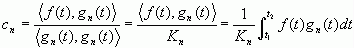 (2-7)
(2-7)
其中, 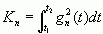 为非零常数。将式(2-7)代入(2-6)中,得最小的均方误差为
为非零常数。将式(2-7)代入(2-6)中,得最小的均方误差为
 (2-8)
(2-8)
若对![]() 有Kn=1 ,即
有Kn=1 ,即![]() ,则该函数集称为归一化正交函数集,此时,相应的各系数和均方误差为:
,则该函数集称为归一化正交函数集,此时,相应的各系数和均方误差为:

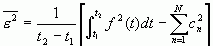 (2-9)
(2-9)
2.3.4 正交复变函数集
以上的讨论仅限于实函数或实信号,下面我们来看看复变函数的正交条件。
若所讨论的函数![]() 和
和![]() 是实变量t的复变函数,则这两个复变函数在区间
是实变量t的复变函数,则这两个复变函数在区间![]() 内相互正交的条件为
内相互正交的条件为
![]()
若![]() 在区间
在区间![]() 内由C12f2(t)来表示,即
内由C12f2(t)来表示,即
![]() 则使均方误差最小的C12值为
则使均方误差最小的C12值为
 (2-10)
(2-10)
如果在区间![]() 内,复变函数集
内,复变函数集 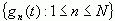 满足
满足
 (2-11)
(2-11)
其中, 则称此函数集为正交复变函数集。
则称此函数集为正交复变函数集。
2.2.5 完备正交函数集
前面我们学习了"信号可以用正交函数集内的所有正交函数的线性组合来近似",但我们还存在一些疑问没有解决:(1)
是否存在一个"完备的"正交函数集,即在此函数集外,没有函数与集内所有函数都正交。(2) 是否存在一个"精确的"正交函数集,即通过集内所有函数的线性组合,可以精确地表示任意信号?这些问题的回答,实际上涉及到了完备正交函数集的两种定义。下面我们来看看。
定义1:已知 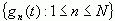 为正交函数集,若不存在函数x(t)能满足
为正交函数集,若不存在函数x(t)能满足
![]()
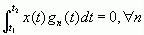
则称此函数集为完备的正交函数集。
显然可见,这种定义强调的是函数集合的"完全性",即集合"囊括"了所有的正交函数,是"完完全全的"。
显然,若能找到这样的函数,则就它归入正交函数集中,于是该函数集就不完备了。若找不到,则函数集就是完备的。
大家看,这个定义,实际上正是根据我们前面提出的第一个疑问来定义的。那么这样的集合到底有没有呢?当然是有的!后面我们会看到相应的例子。
那有人就会问了,若根据第二个疑问,又该如何来定义所谓的完备正交函数集呢?好,下面我们来看关于完备正交函数集的第二种定义方法。
定义2:用正交函数集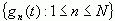 在
在![]() 内表示函数f(t)
内表示函数f(t)
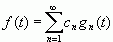 (2-12)
(2-12)
均方误差为
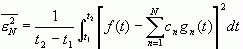
若![]() ,则称
,则称 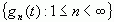 为完备的正交函数集。此时有:
为完备的正交函数集。此时有:
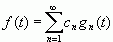 (2-13)
(2-13)
当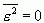 时,由式(2-8)立即可以得到
时,由式(2-8)立即可以得到
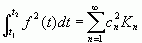 (2-14a)
(2-14a)
如果是归一化完备正交函数集,则
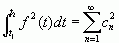 (2-14b)
(2-14b)
式(2-14)也被称为帕斯瓦尔方程,或帕斯瓦尔定理。此方程式表明,一信号所包含的功率等于此信号在完备正交函数集中各分量功率之总和,也即信号用不同方式表示时其能量是守恒的,功率不变。如果上述关系不成立,则正交函数集就是不完备的。
于是乎,从完备正交函数集的特性出发,我们证明了帕斯瓦尔方程。关于这个方程式,我们还可以用另外一种方法来证明它。
下面给出帕斯瓦尔方程的另外一种证明。
证明:由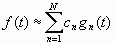 ,可得
,可得
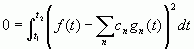
将积分项中差的平方展开,得
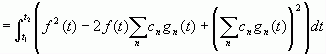
根据积分运算的可加性,把上式中的各积分子项分开,如下
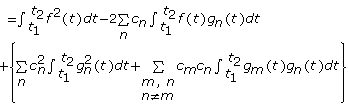
由式(2-7)得
![]()
![]() ,
,
由函数集是正交的可得
![]()
于是有

整理合并可得
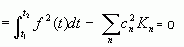
于是可得

有了这些关于完备正交函数集的定义,我们后面将来看看几个完备正交函数集的例子,以及如何用它们对信号进行正交函数分解。
2.2.6 信号分解为完备正交函数
在某一时间段内的信号可以利用完备正交函数集的各分量的线性组合来表示。三角函数集和复指数函数集是应用很广泛的完备正交函数集。通常,可将一周期信号展开为三角函数分量的叠加。
这正是本章将讨论的傅里叶分析的基础所在。
但是大家要注意,完备正交函数集不是仅此一家,别无分店,而是有很多种。如贝塞尔(Bessel)函数集,沃尔什(Walsh)函数集,拉盖尔(Laguerre)函数集,勒让德(Legendre)多项式集,雅可比多项式集和切比雪夫多项式集等属完备的正交函数集。
然而,完备正交函数集不限于三角函数集,还有许多种,不过限于篇幅,我们只讨论三角函数集和复指数函数集。
当然,如果大家对这些知识比较感兴趣,可以去阅读相关的数学书籍。
(1) 三角函数集
三角函数集![]() 在区间
在区间![]() 内组成完备正交函数集,其中T1=2p/w1。
内组成完备正交函数集,其中T1=2p/w1。
下面我们来看看为什么说它是完备的正交函数集?证明一下。
这是由于![]() 满足了完备正交函数集的要求:
满足了完备正交函数集的要求:

好,下面我们来看看信号是如何用这个完备正交函数集来表示的。
对于周期为![]() 的周期函数f(t),可以由上述三角函数的线性组合来表示,即
的周期函数f(t),可以由上述三角函数的线性组合来表示,即
 ,
,![]() (2-15)
(2-15)
通常把上式称为f(t)的傅里叶级数展开,简写为FS。式中系数an、bn可利用式(2-7)求得。
需要指出的是,并非任意周期信号都能进行傅里叶级数展开,周期函数必须满足如下条件才能进行傅里叶级数展开,这些条件称这狄义赫利条件:
(a) 在任一周期内,信号f(t)的间断点的个数有限,而且在这些不连续点上,函数必须是有限值。
(b) 在任一周期内,信号f(t)的最大值和最小值的数目有限。
(c) 在任一周期内,信号f(t)必须是绝对可积的,即 。绝对可积的意思就是说:"绝对"值是"可"以"积"分的,积分结果是有限值。
。绝对可积的意思就是说:"绝对"值是"可"以"积"分的,积分结果是有限值。
那什么样的信号满足上面的条件呢?大家不要担心,通常,我们遇到的周期信号一般都能满足狄义赫利条件。
(2) 复指数函数集
函数集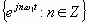 是一个复变函数集,它在区间
是一个复变函数集,它在区间![]() 内是一个完备正交函数集,其中
内是一个完备正交函数集,其中![]() 。
。
同样的,我们要证明一下,为什么它是完备正交函数集?
对复指数函数集可求得
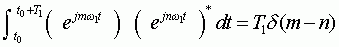
即它是满足对完备正交集的要求的。
因为从某种意义上讲,复指数函数与三角函数在本质上是一致的,所以,能展开成三角函数的无穷级数的周期信号都应能展开成复指数函数的无穷级数。
满足狄义赫利条件的周期函数f(t)可展开为复指数形式傅里叶级数,即
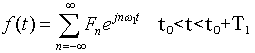 (2-16)
(2-16)
其中,Fn一般是复数。f(t)既可以是复信号,也可以是实信号。
好啦,关于这些系数的求法,以及相互之间的关系,我们在后面再详述。
关于系数an、bn和Fn的求法,以及它们之间的关系,我们将在下一节中详述。