将信号分解为正交函数分量的问题与将矢量分解为正交矢量的方法是类似的。下面我们首先从正交矢量开始讨论,进而引入正交函数集的概念。
好,为了给出正交函数的概念,并研究正交函数的分解方法,下面我们首先来回顾一下矢量的正交矢量分解。
2.2.1 正交矢量
设矢量 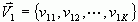 与矢量
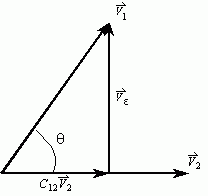
与矢量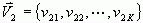 的关系如下图所示其中,
的关系如下图所示其中, 是它们的夹角,
是它们的夹角,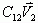 是
是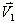 在
在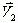 上的投影,
上的投影,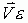 是用投影来表示
是用投影来表示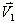 时的误差。由于直角边长小于斜边长,所以根据投影误差可知:如果要用
时的误差。由于直角边长小于斜边长,所以根据投影误差可知:如果要用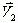 上的矢量来表示
上的矢量来表示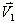 ,则应选择
,则应选择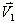 在
在
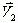 上的垂直投影,这时的投影误差最小。
上的垂直投影,这时的投影误差最小。
此时(选择垂直投影来表示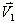 ),
),
![]()
于是,可以求出系数 为
为
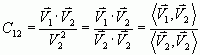
式中的![]() 算子表示求两矢量的内积,定义如下
算子表示求两矢量的内积,定义如下
系数C12表示的是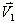 与
与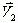 的近似程度。当
的近似程度。当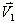 与
与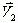 重合时,
重合时, =0,
=0,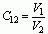 =1;随着
=1;随着![]() 增大,C12减小;当
增大,C12减小;当
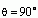 时,C12,此时
时,C12,此时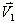 与
与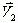 成为相互垂直的矢量,称为正交矢量。
成为相互垂直的矢量,称为正交矢量。
这样,我们就提出这样一个结论:
两个矢量是正交的充要条件是它们的内积为0,即
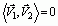 <=>
<=> 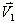 与
与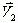 垂直或正交
垂直或正交
下面我们来看看,有了正交矢量后,对我们到底有什么好处?
对于二维平面上的矢量V在直角坐标中可分解为x方向的分量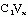 和y方向上的分量
和y方向上的分量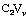 ,其中Vx、Vy表示x和y方向上的正交单位矢量,即
,其中Vx、Vy表示x和y方向上的正交单位矢量,即
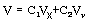
为了便于研究矢量分解,把相互正交的两个矢量组成一个二维正交矢量集,在此平面上的任意矢量均可用二维正交矢量集的分量组合来表示。
同样,对于三维矢量V,也可以用一个三维正交矢量集{Vx,Vy,Vz}的分量组合来表示,即
V = C1Vx+C2Vy+C3Vz
根据此原理,可以把K维空间中的任一矢量 分解为K个互相正交的矢量的和。
2.2.2 正交函数
下面我们来考虑在区间(t1,t2,)内用函数![]() 来近似表示
来近似表示![]() ,即
,即
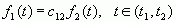
此时,所选择的C12应使得C12ƒ2(t)与ƒ1(t)之间的均方误差
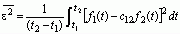
最小。
为求使均方误差最小时的C12,须使 ![]() 。即
。即

交换微分与积分次序,可得

上式中的第一项为零,因此
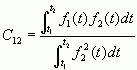 (2-2)
(2-2)
仿照矢量内积定义,定义两个函数![]() 和
和![]() 在区间
在区间![]() 上的内积为
上的内积为
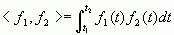
则式(2-2)可以改写为
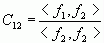 (2-3)
(2-3)
可以看出,它与矢量正交分解的系数公式(2-1)很相似。
和正交矢量的定义类似,当C12=0时,则称![]() 与
与![]() 在区间
在区间![]() 内正交。由式(2-3)可知,两函数在区间
内正交。由式(2-3)可知,两函数在区间![]() 内正交的充要条件是它们的内积为0,即
内正交的充要条件是它们的内积为0,即
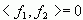
当两个函数正交时C12=C12=0。