任一信号
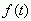 可以分解为直流分量
可以分解为直流分量 和交流分量
和交流分量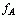 (t)之和,即
(t)之和,即其中信号的直流分量 即信号的平均值。
那么怎么求信号的交流分量呢?从原信号中去掉直流分量即得到信号的交流分量
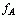 (t)啦。
(t)啦。
1.6.2 偶分量与奇分量
任一信号f(t)都可以分解为偶分量fe(t)都奇分量f0(t)都和,即
f(t)=fg(t)+ f0(t)
其中,偶分量满足fe(t)=fe(-t),而奇分量满足f0(t)=f0(-t),
| 偶分量fe(t)=可表示为: | |
| 奇分量ƒ0(t)可表示为: |
1.6.3 实部分量与虚部分量
任一信号ƒ(t)可以分解为实部分量ƒr(t)和虚部分量ƒi(t)之和,即

根据有关复数的实部、虚部以及共轭运算的知识,可以得到信号的实部和虚部分量分别为

复信号f(t)的模的平方,等于该信号与其自身共轭的乘积,也等于实部和虚部的平方和。即
![]()
虽然实际产生的信号都为实信号,复信号不存在,但是在信号分析理论中,常常借助复信号来研究某些实信号的问题,利用它可以简化运算。复信号在通信系统、网络理论、信号处理等方面的应用非常广泛。
1.6.4 脉冲分量
任一信号可以近似地分解为许多矩形脉冲的叠加,如下图所示:
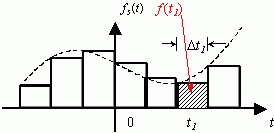
信号的脉冲分解
根据上图,可以写出在![]() 处宽度为
处宽度为![]() 的矩形脉冲分量的表示式为
的矩形脉冲分量的表示式为
![]()
于是,相应的原始信号可表示为
![]()
把脉冲分量的表达式代入上式,可以进一步地得到

通过取极限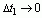 ,可以将上式中的
,可以将上式中的![]() 变成了"=",即
变成了"=",即
![]()
大家看,这不就是冲激信号的抽样特性的表示式吗?换句话说:通过对信号进行脉冲分量分解,可以验证验证冲激信号的抽样特性。
1.6.5 正交函数分量
如果一个函数可以用一组相互正交的函数的线性组合来表示,我们就称某个正交函数与相应的线性系数的乘积为该函数在该正交函数上的正交分量。
例如:用各次谐波的正弦和余弦信号叠加表示一个矩形脉冲,各正弦、余弦信号就是此矩形脉冲信号的正交函数分量
把信号分解为正交函数分量的方法在信号分析和处理中占有很重要的地位,这是本门课程讨论的重要内容,我们将在后面讲傅里叶级数、傅里叶变换时再进行更详细的介绍。现在大家只要了解有这样一种分解的方法或方式就可以了。