那么，这种运算有哪些重要的性质呢？
下面我们来看看卷积运算的性质。
(a) 交换律
f(t)*h(t)=h(t)*f(t)
此性质可以根据变换积分变量法很容易地加以证明。
证明：
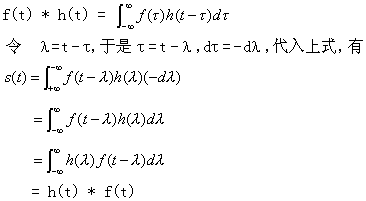
上式表明：在计算卷积积分时，
保持不动，将
反褶、平移后，乘积曲线
下面的面积与不动，将反褶、平移后，乘积曲线
下面的面积是相等的。
此性质表明，两信号在作卷积运算的时候，它们的前后次序是无关紧要的，可以互换，不会改变卷积的结果。
(b) 分配律
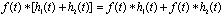
卷积对加法的分配律是积分运算的线性的直接推论。利用积分运算的线性，可以容易地证明此条性质。
证明：
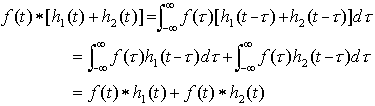
(c) 结合律
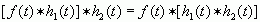
证明：
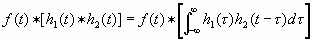
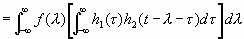
令 
，则 
, 于是上式变为
变换积分次序，上式变成为
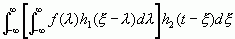
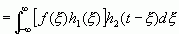
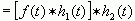
这条性质表明，当多个信号进行卷积运算时，可以随意进行结合，而不会改变结果。这条性质与数值的乘除运算的结合律是相通的。
(d) 卷积的微分
两个信号卷积的微分，等于其中任一信号的微分与另一信号的卷积，即
设y(t)=f(t)*h(t)=h(t)*f(t)，则y'(t)=f(t)*h'(t)=h(t)*f'(t)。
本性质利用求导对于积分的特性，即可证明。
证明：
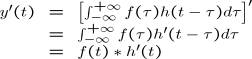
同理
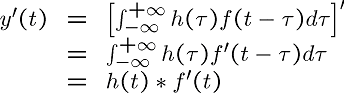
两个信号卷积的积分，等于其中任一信号的积分与另一信号的卷积，即
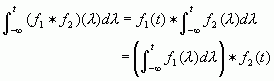
（f）尺度变换
若f(t)=f1(t)*f2(t), 则
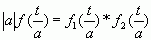，其中a是实数。最后，还需要说明的是，当卷积运算与冲激信号的特性相结合时，会产生很有用的结论。我们将在讲解冲激信号的性质时对此予以详细的讨论。
1.4.5相关运算
设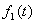
和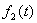
为能量信号，它们的互相关（或相关）运算定义为：
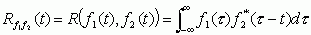
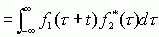
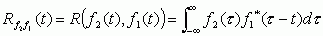
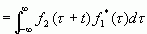
其中，上面两个式子中的右上标"*"，表示复数的共轭运算。从这些定义式，我们可以看出，相关运算的结果与信号的次序是有关的。
当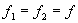
时，一般也称这种运算为自相关运算，简记为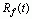
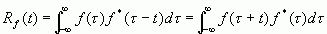
因为是自己和自己进行相关，所以次序就无所谓了。
另外，当f1(t)和f2(t) 均为实函数时，根据实数共轭运算的性质，可以将相关运算改写为：
此时，信号的自相关可以改写为
