1.4.3积分与微分运算
对信号也可以进行积分与微分运算。
可以从两个方面来理解信号的积分与微分运算。
一方面，将信号作为函数来理解，则可以直接把高等数学中所学的积分和微分运算的方法与性质拿过来，这些信号运算和我们学过的信号的其它运算一样，就没有什么特别之处了，无非是些对函数的某种操作而已。
另一方面，如果把信号看成是有着具体的物理背景，则在理解积分与微分运算时，同样应将这些运算与具体的物理意义对应起来来理解。
信号f(t)的积分为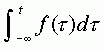
，微分为
。为了叙述方便，有时也把微分和积分运算看成是算子，并分别记为
。
这里，算子的操作对象是函数，结果也是函数，当操作对象是函数f时，微分和积分算子操作的结果就是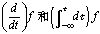 
，写成含有自变量表示的形式就是
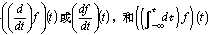。这样，对一个函数连续n次施加微分和积分运算的算子可以分别表示为
。
1.4.4 卷积运算
信号的卷积运算是信号处理领域中最重要的运算之一。随着对信号与系统理论研究的深入，特别是计算机技术的不断发展，不仅使卷积方法在很我领域得到了很广泛的应用，而且卷积运算的逆运算---反卷积的问题也受到了越来越大的重视和应用。
比如，在语音识别、地震勘探、超声诊断、光学成像、系统辨识及其他诸多信号处理领域中，甚至可以说卷积与反卷积的问题无处不在，而且很多的问题，都是有待深入研究的课题。
所以，大家要切实理解和掌握好卷积分运算的各个方面，打好牢固的基础。下面，我们来看看卷积的定义是怎样的。
信号
的卷积积分（简称卷积），定义为：
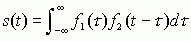
简记为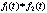
，其中的星号是卷积运算符。注意不要与我们在编写计算机程序时所用的乘法的表示符号搞混了。在信号处理课程里，乘法往往是用居中的点来表示的，或者干脆不写居中的点，而直接将要进行乘积运算的信号(包括直流信号---它是一个常数)连在一起写。
信号的卷积运算对应着一定的物理背景，这要在我们进一步学习了关于系统的激励与响应的关系之后，才能更深入地理解。
不仅如此，信号的卷积运算还对应着一定的几何解释。从定义式我们可以看出：(1) 在积分式中，信号
自变量改变了符号，这对应在几何波形上，就是将信号进行了反褶变换；(2)
并且，信号f2的波形位置与积分变量的取值有关，积分变量在积分限内的不断变化，将导致信号的波形发生移动，即是对它不断进行平移操作；(3)
最后，每当信号处在一个新位置，都要与信号f1相乘，且依据积分的定义，要将这些乘积加起来，而其结果实际上对应着两信号波形相交部分的面积。所以，卷积运算可以用几何图解方式来直观求解。
下面我们来说明如何用它的几何意义来求解两信号
的卷积。
将信号的自变量改为
，信号变为
。对任意给定的
，卷积的计算过程为：
(b) 将 
关于ｒ进行反褶得到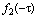
；
(c) 再平移至ｔ0得到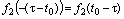
；
(d) 与
相乘得到
；
(e) 对ｒ进行积分得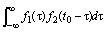
，即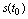
；
不断变化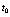，就可以得到s(t)。
从上面的计算步骤可以看出：卷积计算的几何求解可以通过对信号进行"反褶、平移、相乘、积分"等运算来完成。下面我们以一个实例进一步阐述信号之间卷积运算过程的几何解释。
例：下面是矩形脉冲信号e(t)的波形和三角信号h(t)的波形，试根据卷积运算的几何解释求它们的卷积。
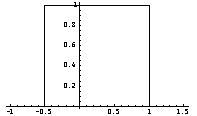
矩形脉冲信号e(t)
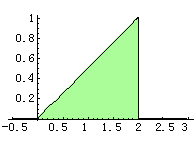
三角脉冲信号h(t)
解：下面按照卷积运算的几何解释以图解方式来求解。
(1) 首先将h(t)反褶
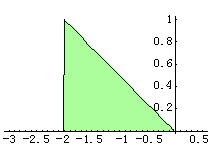
(2) 然后将h(t)沿时间t轴从左向右平移
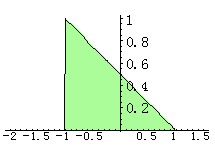
(3) 在平移过程中，将反褶后的h(t)与e(t)相乘相加(积分)
根据h(t)与e(t)之间的位置关系，分阶段求积分结果。也就是两信号波形相交部分的面积随时间变换的函数关系。
(a)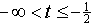 
这时，两个信号的波形没有相交，也即两信号在此区间内的卷积为零。
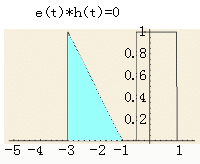
(b)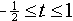 
在此区间内，两信号相交的部分组成一个三角形。在确定了积分的上限和下限后，可以计算出相应的卷积结果如下：
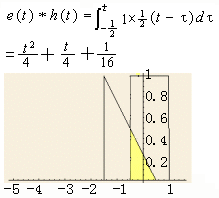
上图中的黄色三角形表示两信号的相交部分，其面积随时间的变化关系即为卷积在此区间内的结果。
(c)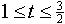 
在此区间内，两信号相交的部分组成了一个梯形，该梯形的面积随着三角波的右移而不断增加，其相应的卷积结果如下：
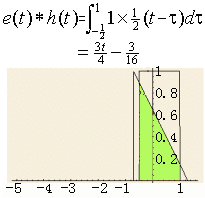
同样的，上图中的红色梯形表示两信号的相交部分，其面积随时间的变化关系即为卷积在此区间内的结果。
(d)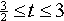 
在此区间内，两信号的相交部分也是梯形，但面积将随时间不断减小，其卷积面积与时间的关系如下：
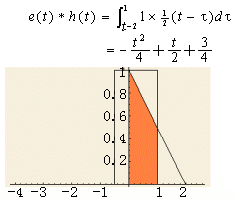
同理，上图中的桔色梯形表示两信号的相交部分，其面积随时间的变化关系即为卷积在此区间内的结果。
(e)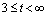 
此时，两信号再一次远离，不再相交，所以卷积结果为零。
e(t)*h(t)=0
(4) 最后的卷积结果为：
综合前面几步的结果，可以绘出下面的卷积的波形如下。
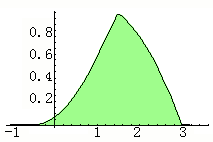
要强调指出的是，卷积作为信号的一种运算，其结果仍是一种信号，描述的是卷积过程中所得面积随时间的变化关系。