1.4.2时移、尺度与反褶运算

　　这几类信号运算，都是在对函数的自变量进行变换，或加上一个常数偏移(时移)，或乘上一个常数作比例系数(尺度)，或改变变量的符号(反褶)。它们的作用效果能够从原信号的波形变化上很直观地看出。

　　信号的波形是原信号f(t)的波形沿时间轴整体平移的结果，我们称这一过程为信号的时移。时移量为，方向与的符号有关。
下图是关于信号时移的两个示例。一个左移，另一个是右移。我们发现，时移操作不会改变信号的波形形状，只改变了它在时间轴上的位置。

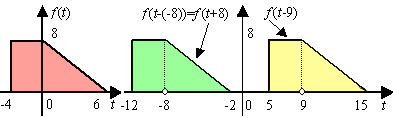
　　如果是正的，则时移将使信号向右平移；反之，则向左平移。如果新信号是，则结论又正好相反。当向右平移时，通常是使得信号发生的时刻延迟了，所以有时也称此运算操作之为"延时"，而将参数称为"时延"。

　　如果将信号f(t)的自变量t乘以一个正的实系数a，则新信号f(at)的波形与原信号的波形有压缩（a>1）或扩展（a<1）的关系。我们称这种运算为尺度运算（有时也称尺度变换、压扩运算、压扩变换）。

　　下图是关于波形压缩(a=2)、波形扩张(a=0.5)的示例。我们可以发现，压扩后的信号与原信号在整体形状上保持了一定的相似性。


　　以放录音磁带为例，设f(t)表示以正常速度播放，则f(2t)表示以两倍的正常速度快放，而f(0.5t)则表示以二分之一的正常速度慢放。

　　如果信号所乘的实系数a=-1，则称新信号f(-t)是原信号的反褶。

　　下图是关于信号反褶的一个示例。我们发现，信号在反褶后波形关于纵轴是对称的。



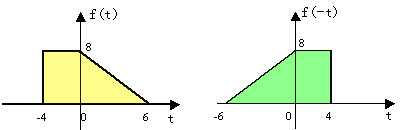
　　这时，f(-t)的波形与f(t)的波形关于纵轴是对称的。换个角度说，对信号进行反褶操作的方法是：将信号以纵轴为对称轴对折过来。

　　如果运算既包含时移运算，又有尺度运算和反褶运算，则如何从原信号得到新信号呢？最简便的方法是：先平移，再压扩，最后反褶。

　　例：已知信号f(t)的波形，试绘出新信号f(-at-b)的波形，其中参数a与b都是正的。

　　解：分三步来完成。

　　(a) 将原信号f(t)的波形沿时间轴向右平移b个单位，得f(t-b)。

　　注意这里了取值是正的，其前面的符号是减号，否则就不一定是向右了。

　　(b) 新信号沿时间轴进行a倍压缩或扩展（视参数a与1的关系来定），得信号f(at-b)。

　　如果参数a大于1，则进行波形压缩；反之则进行波形扩展。

　　(c) 将(b)中所得信号以纵轴为中心对折过来，得信号f(-at-b)即为所求。