1.3.3 复指数信号

　　复指数信号的函数表达式为 。其中是复数s的实部，为其虚部。

　　借助欧拉公式将复指数信号的函数表达式展开，可得

　　

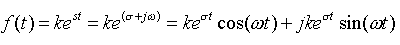
　　欧拉公式我们在其它课程中已经学习过，不知道大家是否记得？下面给出欧拉公式

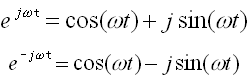
　　此结果表明，一个复指数信号可以分解为实部、虚部两部分。实部含余弦信号，而虚部则是正弦信号。

　　由上面的关系式，我们常将正弦信号和余弦信号借助于复指数信号来表示。利用欧拉公式可推导出

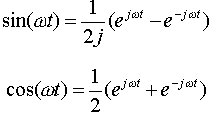
　　这种替换写法有什么意义呢？当我们学习到信号的傅里叶级数展开时会知道，函数(信号)可以展开成正弦函数(信号)的无穷级数表示，而如用复指数函数(信号)来改写该级数，则函数(信号)可以用复指数函数(信号)的无穷级数来表示，从而不仅使表达式更为简捷，带来了复指数信号的优点，而且还便于从傅里叶级数向傅里叶变换的推广。这些，我们将在第二章的相关内容中接触到。

　　不仅如此，利用复指数信号可以使许多运算和分析得以简化。在信号分析理论中，复指数信号是一种非常重要的基本信号。

　　前面我们已经说过，引入复信号是为了方便研究。虽然实际上不能产生复指数信号，但是可以利用复指数信号来描述各种基本信号，如指数信号，正弦或余弦信号，直流信号。

　　复指数信号的指数因子的虚部w表示正弦与余弦信号的角频率，而实部s则表示正弦与余弦函数振幅随时间变化的情况：（1）若> 0，正弦、余弦信号是增幅振荡；（2）若＜0，正弦及余弦是衰减振荡。

　复指数函数有三种特殊情况：
　(1) 当＝0时，即s为虚数，则正弦和余弦信号是等幅振荡；
　(2) 当＝0时，即s为实数，则复指数函数成为一般的指数信号；
　(3) 最后，若＝0且＝0，即s等于零，则复指数信号的实部和虚部都与时间无关，成为直流信号。

1.3.4 高斯信号(钟形脉冲信号)

　　高斯信号的函数表达式是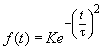,其波形如图所示。

　　由于高斯信号的形状很象一口钟，因此也称为钟形脉冲信号。

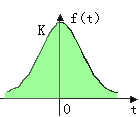
　　该信号在随机信号分析中有重要地位。正态分布的密度函数就是一种高斯函数，我们在对语音信号处理的时候，会大量接触这类信号。

1.3.5 Sa(t)信号(抽样信号)

　　我们把正弦函数sin(t)与自变量t的比值称为抽样函数或Sa(t)函数，其表达式为

　　　　　　　　　　Sa(t) = sin(t)/t
　　其波形如图所示。

　　要注意这个信号在零点处的取值。分式的上下都为零了，怎么办呢？

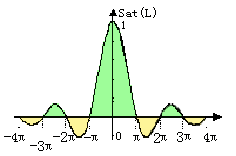
　　当t=0时，Sa(t)函数的分子与分母都是零，借助于罗彼塔法则求得，Sa(0) = 1。当t <> 0时，随着t的绝对值的增大，函数值的绝对值振荡着不断减小，逐渐趋向于零。

　　由于正弦函数sin(t)在 时函数值为0，因此Sa(t)函数在点处函数值为0。通常，我们把相邻两个过零点为端点的区间称为过零区间。

　　显然，除原点附近的过零区间宽度为2外，Sa(t)函数的其他过零区间宽度均为。

　　下面，我们来看看Sa(t)信号还有哪些性质？

　　Sa(t)函数具有下列性质：
　　　1.Sa(t)函数是偶函数。这一点既可以从信号的波形看出，也可以根据偶函数的性质进行证明。
　　　2.
　　　3. 。由前两条性质，本性质很容易证明。

　　鉴于我们在后续章节中还将学习对信号的抽样，为为避免与信号经抽样后所得"抽样信号"（或取样信号、采样信号）相混淆，以后我们将只称Sa(t)信号或Sa(t)函数。

　　另外还有一个类似的函数称为sinc(t)函数，其表达式为