证明：设含因子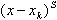的多项式的形式为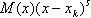，对其求导，可得

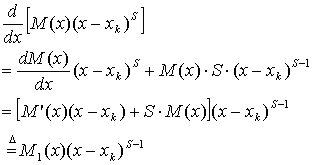(6)

　　式(6)表明：若多项式含有因子，则其一阶导数将含有因子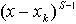。这个求导过程可以不断进行下去，易得：多项式的　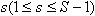阶导数将含有因子。
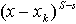　　根据上述结论，我们先对式(5)两边同时乘以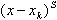，得
　　　　　　　　　　　　　　　　　　(7)

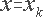　　然后再对式(7)两边求阶导数，并令，则
　　　(1)对项:求导后的结果含有因式，代入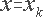后，此项为零；

　　　(2)对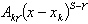各项

　　　　　(a) 若，则求导后含有因式，代入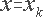后，此类各项为零；

　　　　　(b) 若，则求导后的各项结果均为零；

　　　　　(c) 若，则求导后的结果为。